
大学入試に必ずと言っていいほど出題される微分と積分ですが、多くの生徒が苦手意識を持っています。今回は微分を中心に分かりやすく説明していきたいと思います。
「微分する」とはどういうこと?
微分を学ぶ際にまず出てくるのは、微分係数f’(a)の定義式です。
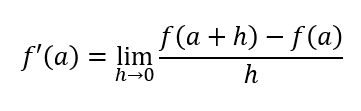
ん~なんだかわけが分かりませんよね。この式を初めて見て、なるほどねって理解できる人はなかなかいないと思います。
これは難しく書いていますが、分母はxの増加量を、分子はf(x)の増加量(つまりyの増加量)を表しており、つまり分数部分は中学校で学習した変化の割合(平均変化率)を示しているだけです。
2次関数を例に図示すると、次のようになります。
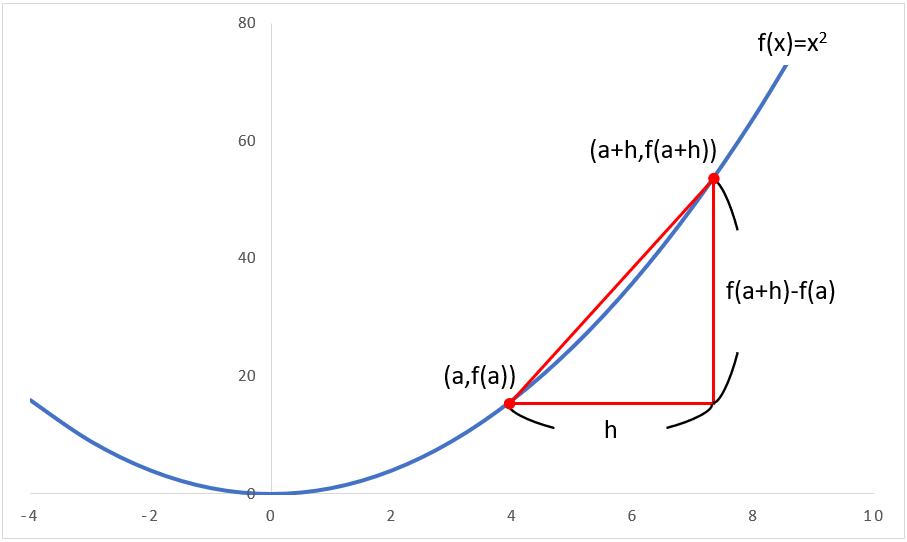
中学校で1次関数を学習した時もそうでしたが、関数は傾きが大事なんです。しかし、上図を見ても分かるように、赤線(斜辺)の傾きは曲線f(x)の傾きを表しているとは言えませんよね。なぜならば、曲線においては、どの点をとるかで傾きが変化するため、xの増加量hに幅がある限りその曲線の傾きを表すことができないからです。
そこで、xの増加量を限りなく0に近づけて(h→0)、点(a,f(a))における傾き=接線の傾きを求めようというのが上の式で、これがx=aで微分する(微分係数を求める)ということになります。
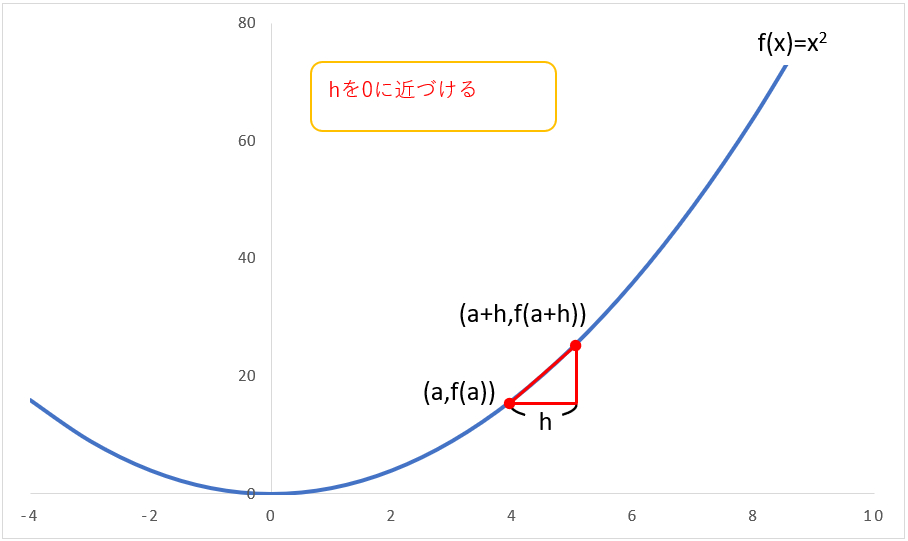
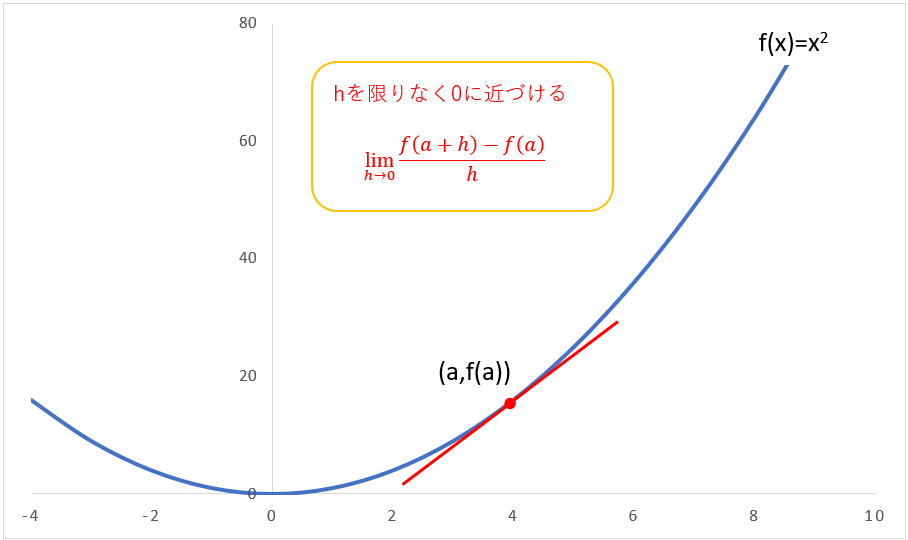
上のグラフで、a=4を例に計算してみると、
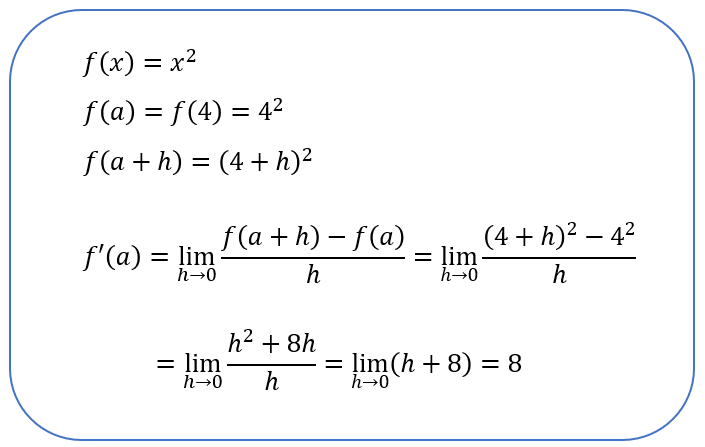
よって、x=4における接線の傾きは、8ということが分かります。導関数の公式を用いても、f’(x)=2xよりf’(4)=8となり、確かですね。
傾きにおいては数字の大小よりも、傾きが正(右上がり)なのか、負(右下がり)なのかが重要になってきます。特に傾きが0の時を極値と呼び、上のグラフの例でみるとx=0の時、傾きが0となり極値(この場合は極小値)をとります。
この傾きの正負および極値を調べることで、未知の複雑な関数に遭遇しても、グラフの概形図が書けるようになります。
グラフが書けると、なんなのさ?
ボール投げ(物理でいうところの斜方投射)を例に見てみましょう。
速さv0、角度θでボールを投げた時に、t秒後のボールの高さyは、
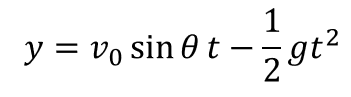
であるということが分かっています。ただし、空気抵抗は考慮しません。
この式を見てもなんかピンときませんが、ボールを斜めに投げると放物線を描いて地面に落ちることは(経験上)想像できると思います。
では、速さ14m/秒(時速50kmくらい)、角度45°でボールを投げた場合、放物線の頂点に到達するのは何秒後で、その高さ(最高点)は何mでしょうか。
y=f(t)とすると、上で述べたように放物線の頂点(極値)はf’(t)=0であるから

よって、投げてから1.0秒後に最高点に達し、その高さは5.0mだということが分かりました。これをグラフ化すると次のようになります。
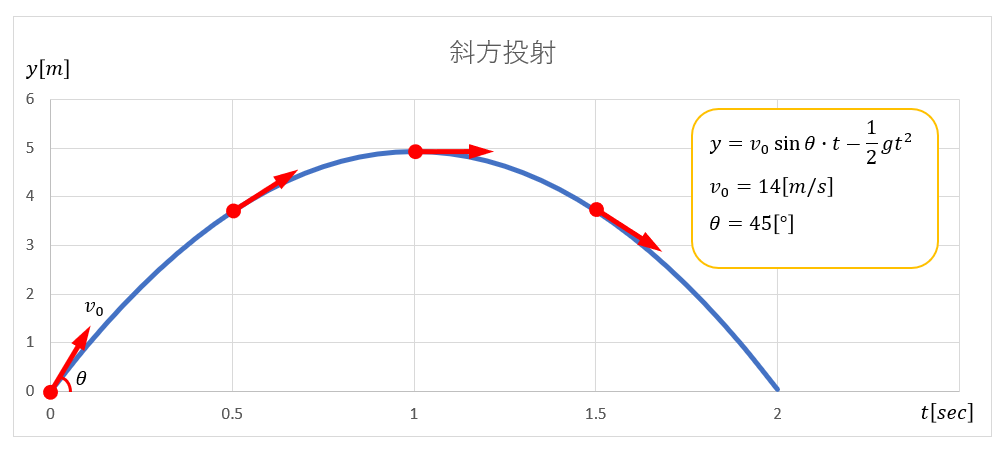
グラフ化すると、ボールを投げて約1秒後に5mほどの高さまで上がり、その後下降に転じて、投げてから約2秒後に地面に落ちる様子がよく分かります。
このように、よく分からない数式でもグラフにすることで、物事の動きやピークが視覚的に理解できるといったケースはたくさんあります。
今回は高さ方向yを例にあげましたが、これを水平方向xに適用すると、角度をどのくらいで投げると一番遠くに投げられるか、100m投げるには初速何m必要か、といったことも求めることができます。
微分・積分は不可欠!
ところで、微分は英語で「differential(ディファレンシャル)」といい、dxやdyの頭文字ですね。積分は「integral(インテグラル)」ですが、「integral」には他に「不可欠な」や「なくてはならない」といった意味があります。
さまざまな物理の法則は微分・積分から成り立っています。上の斜方投射の公式も、実は微分方程式で導くことができるんです。まさに現代の科学において、微分・積分は不可欠な存在だといえます。
さいごに
微分は何に役立つか分からずに、苦手意識を持つ生徒も多いと思います。
“公式を丸暗記すること”ではなく、忘れても導けるように”本質を理解すること“が重要です。
ほんのちょっとした捉え方の違いで、数学力はグッと身につきます。
個別指導塾の「好文館」では日本全国を対象に、微分の他、数学の基礎をオンラインにて個別指導しております。
お問い合わせ後、お電話やZoomにて学習の進み具合や弱点などを教えてください。




