「三角形の面積を求めよ」という問題は、小学校から高校・大学入試、さらには就職試験(SPI)まで、よく見られる問題です。
なぜ三角形の面積がそれほど重要なのでしょうか。それは四角形以上の多角形は三角形に分割することができるので、三角形の面積を求めることができれば、あらゆる多角形の面積(例えば下図のような土地の面積)も求めることができるからです。
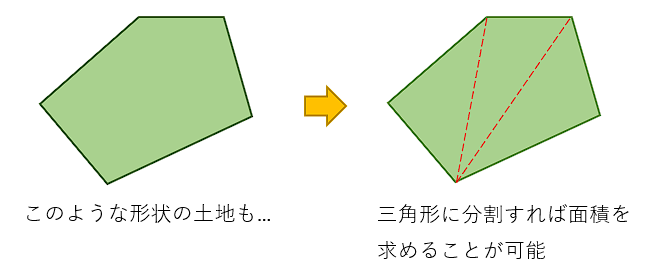
本記事では、小学校で習う基本の公式から、ヘロンの公式・三角比・ベクトルの公式まで、例題を用いて、なるべくわかりやすく解説します。
基本の公式「底辺×高さ÷2」
三角形の面積を求める公式は様々ありますが、全ての公式は小学校で習う「底辺×高さ÷2」が基本となっています。なぜこの公式が成り立つのか考えてみましょう。
前提として、平行四辺形の面積は「底辺×高さ」であることを用います。(以下、底辺と高さは垂直とします)
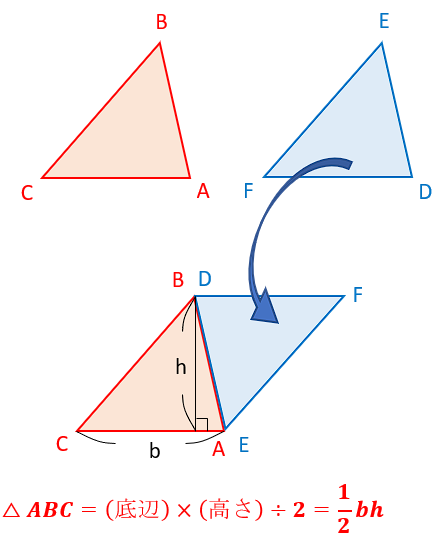
面積を求めたい三角形をABCとし、これと同じ三角形DEF(△ABC≡△DEF)を準備して、頂点AとE、BとDがそれぞれ一致するようにくっつけると、平行四辺形ができます。
この平行四辺形の面積は「底辺×高さ」であることから、元の△ABCの面積はその半分、つまり「底辺×高さ÷2」が成り立つことになります。
3辺が分かっている場合(三平方の定理)
中学校で三平方の定理を学習すると、高さが分かっていなくても3辺の長さが与えられていれば、三角形の面積を求めることが可能です。
この場合は公式として覚えるのではなく、次の例題のような手順を覚えるようにしましょう。
【例題1】△ABCにおいて、3辺の長さがそれぞれ a=13,b=21,c=20のとき、△ABCの面積を求めよ。
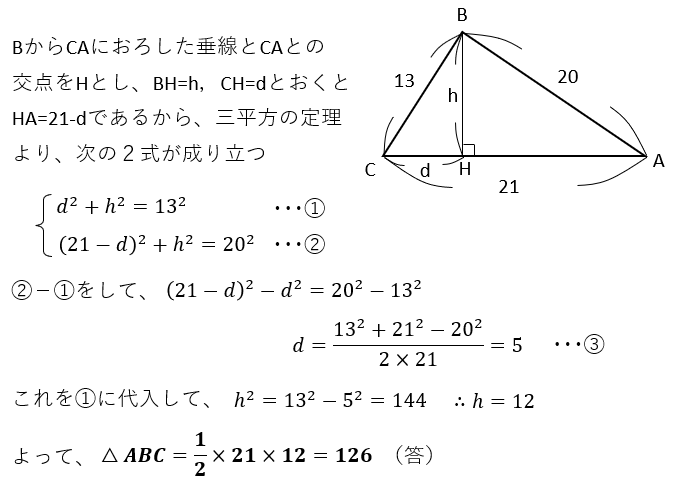
このように、やはり面積を求めるには高さhが必要なわけですが、hを求めるために底辺を分割して直角三角形を2つ作り、それぞれに三平方の定理を適用します。
同様の手順で一般化すると、次の公式が成り立ちます。
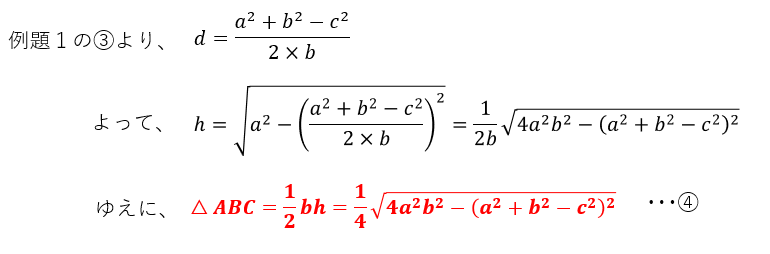
特に正三角形の場合、a=b=cであるから、1辺が与えられていれば面積を求めることが可能です。
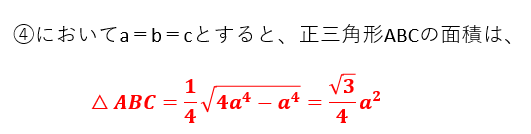
これは公式として覚えておくと便利でしょう。
3辺が分かっている場合(ヘロンの公式)
上記④の公式は実際に計算してみると分かりますが、かなり大変です。そこで④を変形して計算しやすくしたものが「ヘロンの公式」です。

ヘロンの公式を使って【例題1】を解いてみましょう。
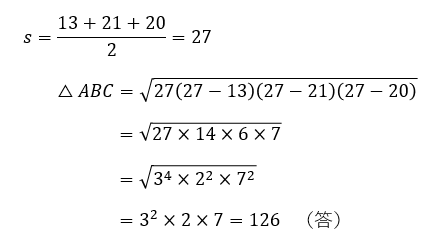
たしかに答えが一致しました。このように、辺の長さがそれぞれ整数(あるいは有理数)であればヘロンの公式が非常に効果的です。しかし、辺の長さに無理数を含んでいると計算が繁雑になるため、三平方の定理を用いた手順の方が楽な場合があります。
内接円の半径が分かっている場合
三角形の3辺の長さに加えて、内接円の半径が分かっている場合、三角形の面積は簡単に求めることができます。
内接円の中心をI、半径をrとすると、△ABC=△IBC+△ICA+△IABである。△IBC,△ICA,△IABの底辺をそれぞれ a,b,cとすると、その高さはいずれもrであることから、次の公式が成り立ちます。
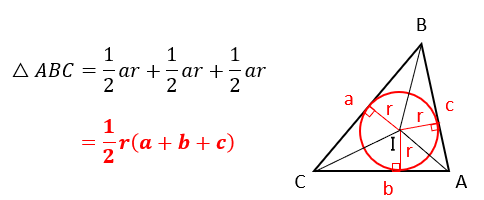
三角比を使った面積の求め方
数学Ⅰで三角比(sin,cos,tan)を学習すると、2辺とその間の角が分かっていれば三角形の面積を求めることができます。
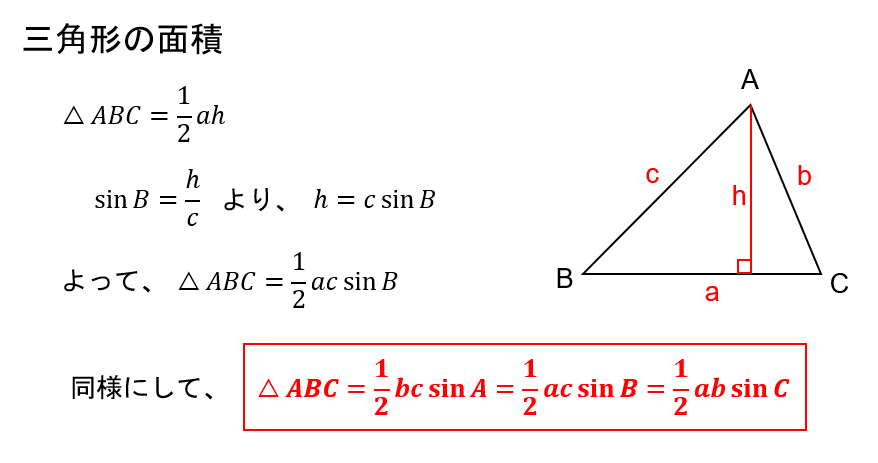
三角比の定義や公式については関連記事を参考にしてください。
関連記事:三角比を数学講師がわかりやすく解説!覚え方・公式・表まで
座標を使った三角形の面積(図形と方程式)
平面座標上の三角形の面積を求めるには、次の公式が効果的です。
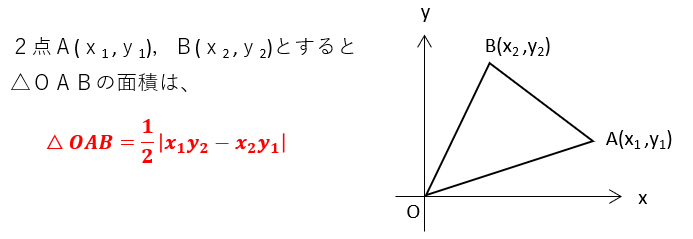
この公式の証明には、数学Ⅱで学習する「点と直線の距離の公式」を使います。
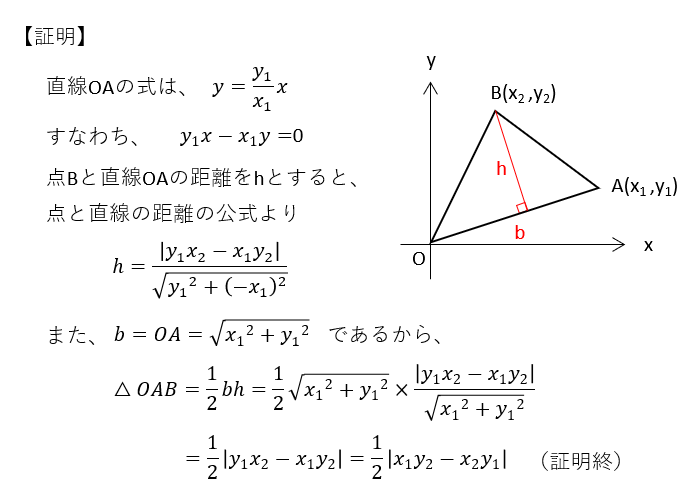
この公式は、三角形の1点が原点になくても、三角形を平行移動して原点にもってくれば適用可能です。例題で見てみましょう。
【例題2】3点A(7,4),B(5,7),C(3,3)を頂点とする△ABCの面積を求めよ。
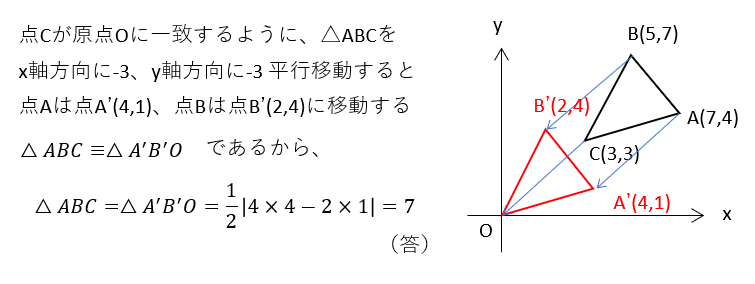
ベクトルを使った三角形の面積
上記の三角比を用いた面積の公式と、ベクトルの内積を利用して、三角形の面積をベクトルで表すと下記のようになります。
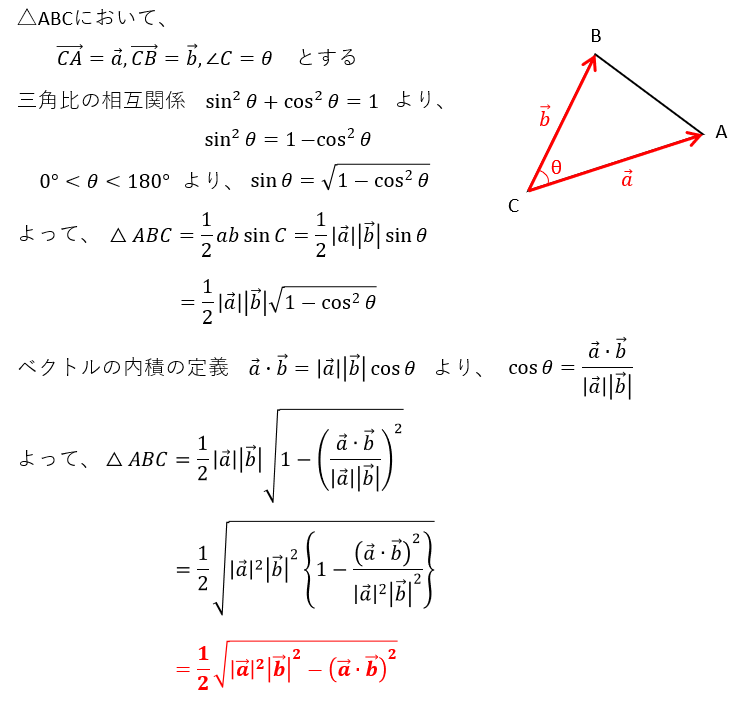
この公式は一見覚えにくいですが、ベクトルの成分が分かれば角度を求める必要がなく、また平面座標だけでなく空間座標にも適用できるので非常に便利です。例題で見てみましょう。
【例題3】空間に3点A(0,2,1),B(2,3,2),C(-2,4,-3)がある。△ABCの面積を求めよ。
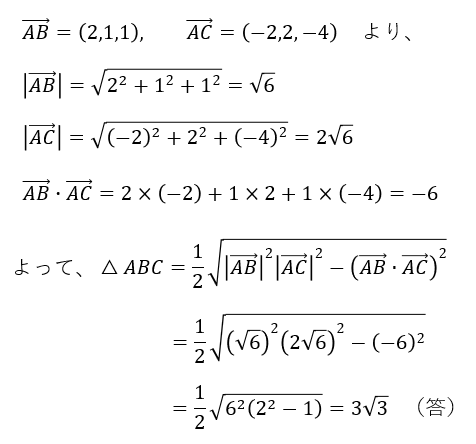
このように、図示することが難しい空間座標でも機械的に求めることができるのが、ベクトルの強みです。
さいごに
今回は三角形の面積に焦点を当てて、小学校の基本の公式から高校の三角比・ベクトルを使った公式まで紹介しました。
重要なのは、”公式を丸暗記すること”ではなく、忘れても導けるように”本質を理解すること“です。
ほんのちょっとした捉え方の違いで、数学力はグッと身につきます。
個別指導塾の「好文館」では日本全国を対象に、数学の基礎をオンラインにて個別指導しております。
お問い合わせ後、お電話やZoomにて学習の進み具合や弱点などを教えてください。




