三角比は覚えることが多く、苦手意識を持つ生徒も多いと思います。
重要なのは、公式を丸暗記するのではなく、忘れても導けるように”本質を理解すること“です。
本記事では三角比の基本・覚え方・公式について、数学講師が成り立ちや導き方を解説します。
三角比とは?
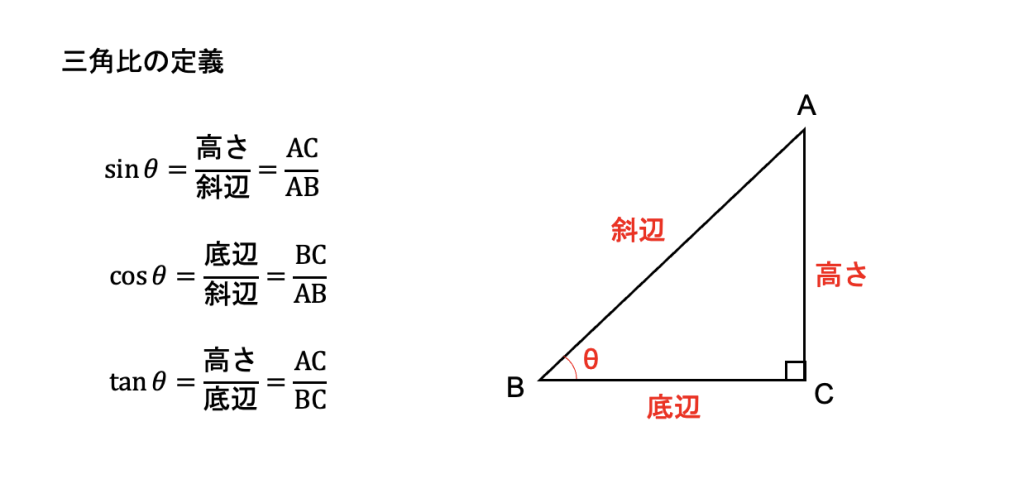
三角比とは、三角形の辺の比のことです。
直角三角形の斜辺(一番長い辺)と高さの比を正弦(サイン)、斜辺と底辺の比を余弦(コサイン)、底辺と高さの比を正接(タンジェント)と呼び、次のように表します。
三角比の覚え方
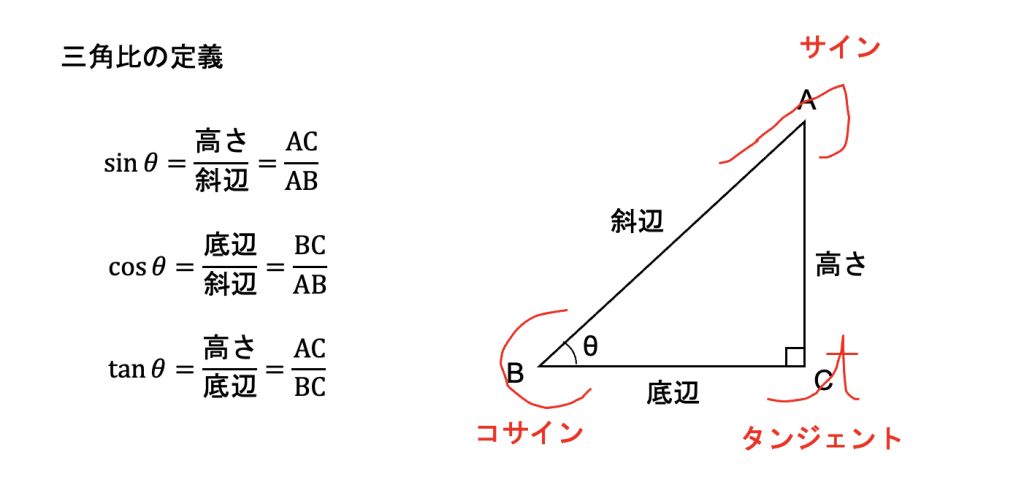
それぞれの頭文字 s,c,t の筆記体の書き順で、分母→分子と覚えるとよいでしょう。
三角比の基本
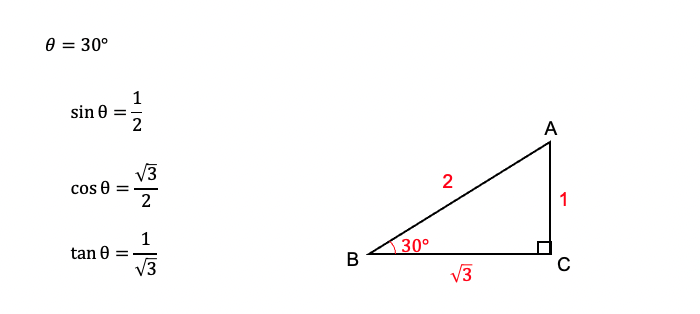
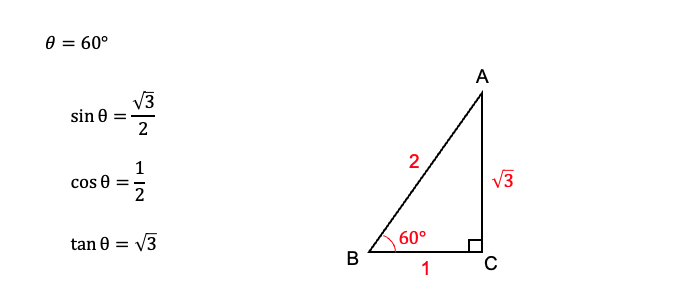
三角定規に用いられる、30°・45°・60°の三角比が基本となります。
これらは高校数学でよく用いられるので、必ず覚えましょう。
30°の三角比
45°の三角比
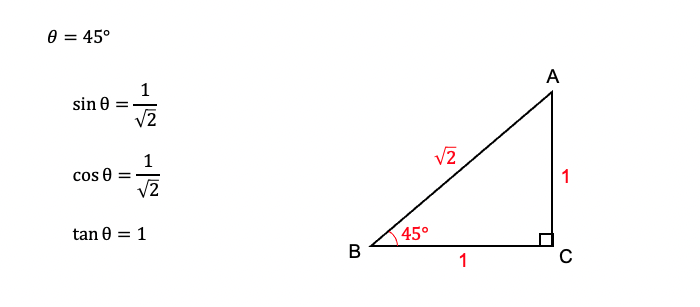
60°の三角比
三角比の公式(三角比の相互関係)
三角比の定義から次の公式が導かれます。
いずれも重要公式なので、覚えておきましょう。
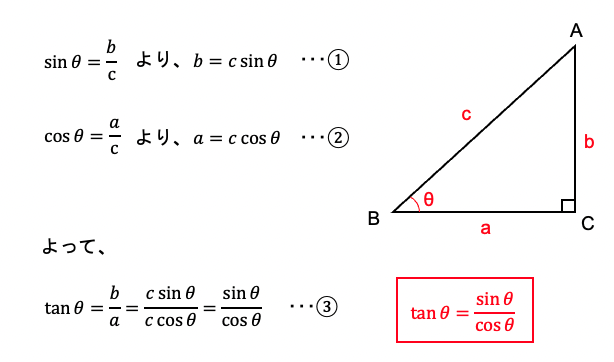


これらの公式を使うことにより、sinθ,cosθ,tanθ のいずれか1つの値が分かると、その他の値を求めることができます。
三角比の拡張
三角比は座標として捉えることで、θが鋭角(0°<θ<90°)の場合だけでなく、鈍角を含め、あらゆる角度で扱うことができます。
また、上記の公式、相互関係も同様に成り立ちます。
θ=120°の場合を見てみましょう。
原点を中心とする半径1の円を考えたとき、x軸の正の方向から120°回転させた直線と円との交点Aは第二象限となります。
第二象限には60°の直角三角形(1:2:√3)ができることから、点Aの座標は下図の通りとなり、これに上記の三角比の定義を適用させると、次のようになります。
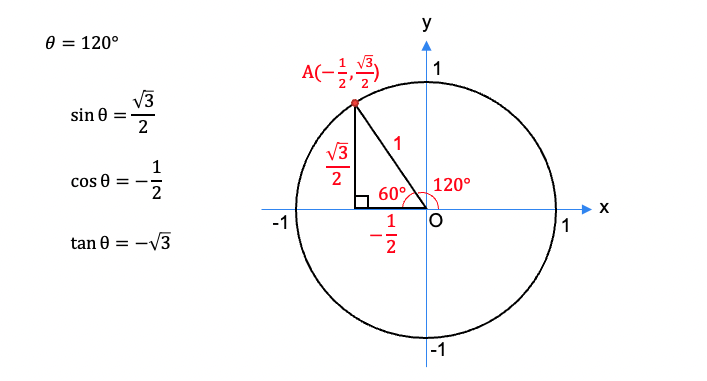
このように、cosθがx座標、sinθがy座標に対応しています。
また、tanθはsinθ/cosθなので、y/xとなり、直線OAの傾きを意味しています。
そのように考えると、θ=0°のときは、cosθ=1,sinθ=0,tanθ=0 となります。
θ=90°のときは、sinθ=1,cosθ=0 となり、(分母が0であるため)tanθの値は存在しません。
同様にして、θ=90°,135°,150°,180°を求めると、次の表が完成します。
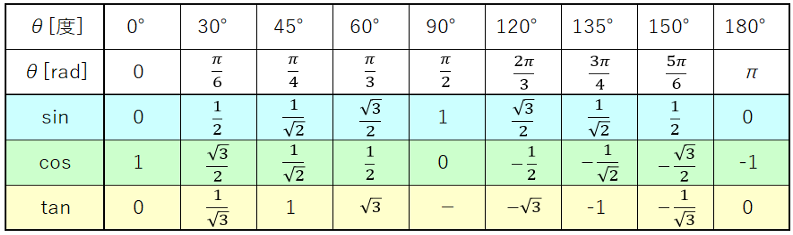
※弧度法[rad]は数学Ⅱで学習します
正弦定理と余弦定理
三角形には3辺と3つの角、合わせて6つの要素がありますが、その内 1辺を含む3つの要素が分かっていれば、その他の要素は、正弦定理と余弦定理を用いて求めることができます。
正弦定理は正弦(sin)に関する定理で、△ABCの外接円の半径をRとすると、次の等式が成り立ちます。
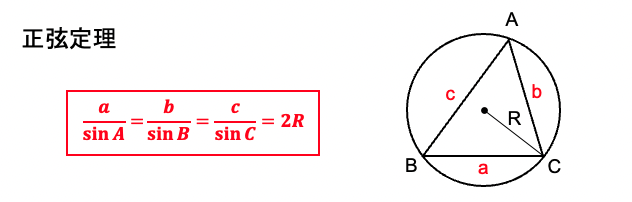
1辺2角が与えられている場合は正弦定理を使いましょう。
余弦定理は余弦(cos)に関する定理で、2辺1角 または 3辺が与えられている場合は余弦定理を使いましょう。
関連記事:正弦定理と余弦定理の公式・証明・例題を数学講師がわかりやすく解説
三角比を使った面積の求め方
中学生までは三角形の面積の公式は、「(底辺)×(高さ)÷ 2」でした。
三角比を学習すると、高さが与えられていなくても、2辺とその間の角が分かっていれば三角比より求めることができます。
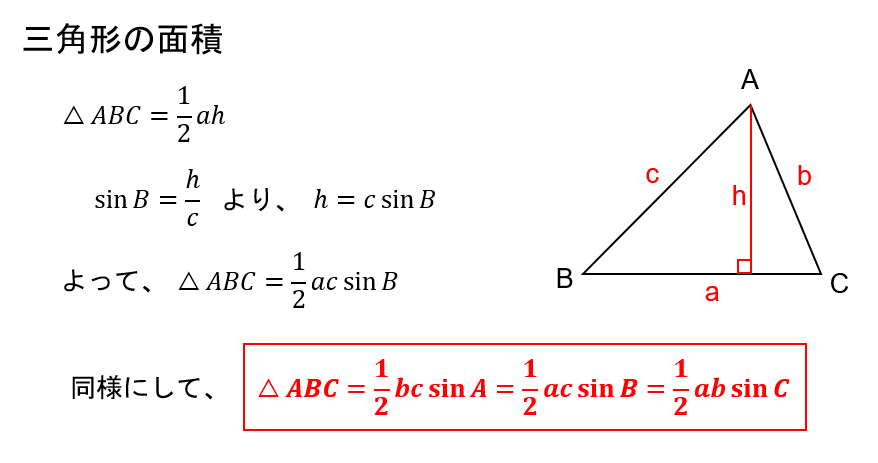
下図の△ABCにおいて高さをhとすると、h=c・sinB と表すことができます。よって、下記の公式が成り立ちます。
さらに、正弦定理・余弦定理や三角比の公式を組み合わせることによって、3つの要素(1辺を含む)が分かっていれば、面積を求めることができます。
三角形の面積の例題
以上の公式を使って、三角形の面積を求めてみましょう。
【例題】△ABCにおいて、a=2,b=3,c=4のとき、面積Sを求めよ。
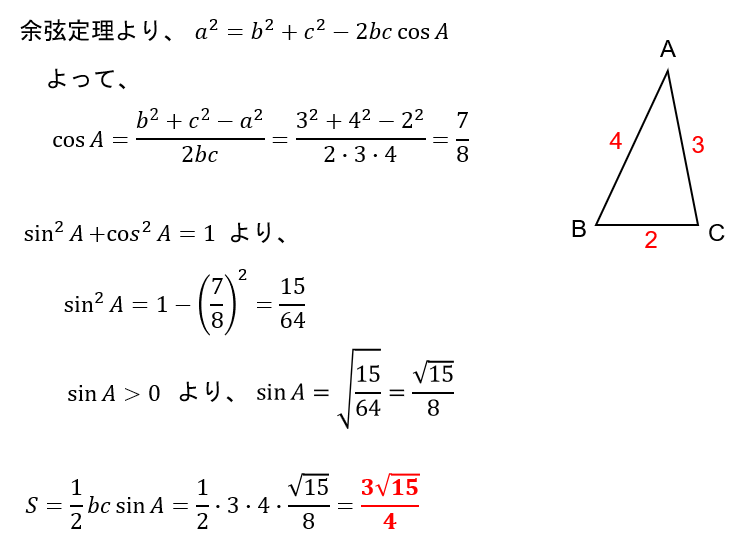
この例題のように、3辺が与えられている場合の面積の求め方は3ステップです。
➀余弦定理を使っていずれかのcos■を求める(■はどの角でもよい)
➁相互関係を用いてsin■を求める(sin■>0)
③sin■を用いた面積の公式に当てはめる
関連記事:三角形の面積の求め方を数学講師が解説!小学校から高校の公式まで
さいごに
三角比は覚えることが多く、苦手意識を持つ生徒も多いと思います。
冒頭でもお伝えした通り、”公式を丸暗記すること”ではなく、忘れても導けるように”本質を理解すること“が重要です。
ほんのちょっとした捉え方の違いで、数学力はグッと身につきます。
個別指導塾の「好文館」では日本全国を対象に、三角比の他、数学の基礎をオンラインにて個別指導しております。
お問い合わせ後、お電話やZoomにて学習の進み具合や弱点などを教えてください。